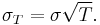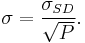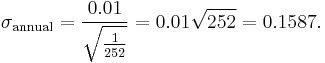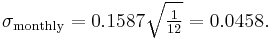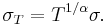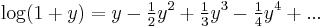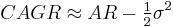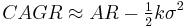Volatility (finance)
In finance, volatility is a measure for variation of price of a financial instrument over time. Historic volatility is derived from time series of past market prices. An implied volatility is derived from the market price of a market traded derivative (in particular an option).
It is common for discussions to talk about the volatility of a security's price, even while it is the returns' volatility that is being measured. It is used to quantify the risk of the financial instrument over the specified time period. Volatility is normally expressed in annualized terms, and it may either be an absolute number ($5) or a fraction of the mean (5%).
Contents |
Volatility terminology
Volatility as described here refers to the actual current volatility of a financial instrument for a specified period (for example 30 days or 90 days). It is the volatility of a financial instrument based on historical prices over the specified period with the last observation the most recent price. This phrase is used particularly when it is wished to distinguish between the actual current volatility of an instrument and
- actual historical volatility which refers to the volatility of a financial instrument over a specified period but with the last observation on a date in the past
- actual future volatility which refers to the volatility of a financial instrument over a specified period starting at the current time and ending at a future date (normally the expiry date of an option)
- historical implied volatility which refers to the implied volatility observed from historical prices of the financial instrument (normally options)
- current implied volatility which refers to the implied volatility observed from current prices of the financial instrument
- future implied volatility which refers to the implied volatility observed from future prices of the financial instrument
For a financial instrument whose price follows a Gaussian random walk, or Wiener process, the width of the distribution increases as time increases. This is because there is an increasing probability that the instrument's price will be farther away from the initial price as time increases. However, rather than increase linearly, the volatility increases with the square-root of time as time increases, because some fluctuations are expected to cancel each other out, so the most likely deviation after twice the time will not be twice the distance from zero.
Since observed price changes do not follow Gaussian distributions, others such as the Lévy distribution are often used.[1] These can capture attributes such as "fat tails".
Volatility and Liquidity
Much research has been devoted to modeling and forecasting the volatility of financial returns, and yet few theoretical models explain how volatility comes to exist in the first place.
Easley, López de Prado and O'Hara (2010)[2] argue that at least one source of volatility can be explained by Market microstructure theory, as the result of the liquidity provision process. When market makers infer the possibility of Adverse selection, they adjust their trading ranges, which in turn increases the band of price oscillation. If the level of toxicity surprises market makers, they may opt to vanish from the market altogether, leading to exacerbated price moves such as the so called 2010 Flash Crash.
Volatility for investors
Investors care about volatility for five reasons. 1) The wider the swings in an investment's price the harder emotionally it is to not worry. 2) When certain cash flows from selling a security are needed at a specific future date, higher volatility means a greater chance of a shortfall. 3) Higher volatility of returns while saving for retirement results in a wider distribution of possible final portfolio values. 4) Higher volatility of return when retired gives withdrawals a larger permanent impact on the portfolio's value. 5) Price volatility presents opportunities to buy assets cheaply and sell when overpriced.[3]
In today's markets, it is also possible to trade volatility directly, through the use of derivative securities such as options and variance swaps. See Volatility arbitrage.
Volatility versus direction
Volatility does not measure the direction of price changes, merely their dispersion. This is because when calculating standard deviation (or variance), all differences are squared, so that negative and positive differences are combined into one quantity. Two instruments with different volatilities may have the same expected return, but the instrument with higher volatility will have larger swings in values over a given period of time.
For example, a lower volatility stock may have an expected (average) return of 7%, with annual volatility of 5%. This would indicate returns from approximately negative 3% to positive 17% most of the time (19 times out of 20, or 95% via a two standard deviation rule). A higher volatility stock, with the same expected return of 7% but with annual volatility of 20%, would indicate returns from approximately negative 33% to positive 47% most of the time (19 times out of 20, or 95%). These estimates assume a normal distribution; in reality stocks are found to be leptokurtotic.
Volatility over time
Although the Black Scholes equation assumes predictable constant volatility, none of these are observed in real markets, and amongst the models are Bruno Dupire's Local Volatility, Poisson Process where volatility jumps to new levels with a predictable frequency, and the increasingly popular Heston model of Stochastic Volatility.[4]
It's common knowledge that types of assets experience periods of high and low volatility. That is, during some periods prices go up and down quickly, while during other times they might not seem to move at all.
Periods when prices fall quickly (a crash) are often followed by prices going down even more, or going up by an unusual amount. Also, a time when prices rise quickly (a bubble) may often be followed by prices going up even more, or going down by an unusual amount.
The converse behavior, 'doldrums' can last for a long time as well.
Most typically, extreme movements do not appear 'out of nowhere'; they're presaged by larger movements than usual. This is termed autoregressive conditional heteroskedasticity. Of course, whether such large movements have the same direction, or the opposite, is more difficult to say. And an increase in volatility does not always presage a further increase—the volatility may simply go back down again.
Mathematical definition
The annualized volatility σ is the standard deviation of the instrument's yearly logarithmic returns.[5]
The generalized volatility σT for time horizon T in years is expressed as:
Therefore, if the daily logarithmic returns of a stock have a standard deviation of σSD and the time period of returns is P, the annualized volatility is
A common assumption is that P = 1/252 (there are 252 trading days in any given year). Then, if σSD = 0.01 the annualized volatility is
The monthly volatility (i.e., T = 1/12 of a year) would be
The formula used above to convert returns or volatility measures from one time period to another assume a particular underlying model or process. These formulas are accurate extrapolations of a random walk, or Wiener process, whose steps have finite variance. However, more generally, for natural stochastic processes, the precise relationship between volatility measures for different time periods is more complicated. Some use the Lévy stability exponent α to extrapolate natural processes:
If α = 2 you get the Wiener process scaling relation, but some people believe α < 2 for financial activities such as stocks, indexes and so on. This was discovered by Benoît Mandelbrot, who looked at cotton prices and found that they followed a Lévy alpha-stable distribution with α = 1.7. (See New Scientist, 19 April 1997.)
Crude volatility estimation
Using a simplification of the formulae above it is possible to estimate annualized volatility based solely on approximate observations. Suppose you notice that a market price index, which has a current value near 10,000, has moved about 100 points a day, on average, for many days. This would constitute a 1% daily movement, up or down.
To annualize this, you can use the "rule of 16", that is, multiply by 16 to get 16% as the annual volatility. The rationale for this is that 16 is the square root of 256, which is approximately the number of trading days in a year (252). This also uses the fact that the standard deviation of the sum of n independent variables (with equal standard deviations) is √n times the standard deviation of the individual variables.
Of course, the average magnitude of the observations is merely an approximation of the standard deviation of the market index. Assuming that the market index daily changes are normally distributed with mean zero and standard deviation σ, the expected value of the magnitude of the observations is √(2/π)σ = 0.798σ. The net effect is that this crude approach underestimates the true volatility by about 20%.
Estimate of compound annual growth rate (CAGR)
Consider the Taylor series:
Taking only the first two terms one has:
Realistically, most financial assets have negative skewness and leptokurtosis, so this formula tends to be over-optimistic. Some people use the formula:
for a rough estimate, where k is an empirical factor (typically five to ten).
Criticisms
Despite their sophisticated composition, the predictive power of most volatility forecasting models is similar to that of plain-vanilla measures, such as simple past volatility. The body of work dedicated to volatility forecasting models is overwhelming. Thousands of academics have devoted their entire careers to publishing models that supposedly are able to forecast volatility. Some authors have published well over 40 papers on this very topic,[6] and yet none seems to deliver any improvement over the simple standard deviation.[7][8] Torben Andersen has fiercely attacked skeptics in a number of papers. In Answering the Critics: Yes, ARCH models do provide good volatility forecasts, Andersen and Bollerslev attack the work of leading researchers such as Cumby, Figlewski, Hasbrouck, Jorion among many others, arguing that they do not know how to correctly implement their models.[9] In Answering the Skeptics: Yes, Standard Volatility Models Do Provide Accurate Forecasts, Andersen and Bollerslev again repeat their attack on those who apply Occam's Razor to dismiss volatility forecasting models. It is interesting to note that while critics are publishing their papers in top journals such as Journal of Finance, Journal of Derivatives, Journal of Portfolio Management, etc. those defending their volatility forecasting models or criticizing skeptics have been unable to publish their work in journals of similar prestige, in many cases opting for leaving them unpublished, as working papers.[10]
Besides this controversy between believers in volatility forecasting models and the large majority of skeptics, there is a contentious battle among those same believers, one claiming that his model is superior to the rest. In August 2008, Torben Andersen and Prof. Oleg Bondarenko once again surprised the academic community by claiming not only that their volatility forecasting model was superior, but that they have mathematically demonstrated that future research was futile, since no future volatility forecasting model can beat theirs.[11]
In an interview regarding their CIV model, Andersen and Bondarenko go as far as to assert[12]
| “ | The best possible market-based implied volatility measure for volatility prediction may take the form of a corridor implied volatility (CIV) measure. | ” |
Removed from this controversy, practitioners and portfolio managers seem to completely ignore or dismiss volatility forecasting models. For example, Nassim Taleb famously titled one of his Journal of Portfolio Management papers We Don't Quite Know What We are Talking About When We Talk About Volatility.[13] Nassim Taleb gained worldwide recognition through his Black swan theory, which argues the sillines of trying to predict the unpredictable.
In a similar note, Emanuel Derman expressed his disillusion with the enormous supply of empirical models unsupported by any theory.[14] He argues that, while "theories are attempts to uncover the hidden principles underpinning the world around us, as Albert Einstein did with his theory of relativity", we should remember that "models are metaphors -- analogies that describe one thing relative to another". From that perspective, volatility forecasting models are nothing more than high-tech horoscopes: Even if they were successful predictors (which they are not), they would not add anything to our understanding of the principles governing the markets.
See also
- Beta (finance)
- Derivative (finance)
- Financial economics
- Implied volatility
- IVX
- Risk
- Standard deviation
- Stochastic volatility
- Volatility arbitrage
- Volatility smile
References
- ^ http://www.wilmottwiki.com/wiki/index.php/Levy_distribution
- ^ Easley, D., M. López de Prado and M. O'Hara (2010): "Flow Toxicity and Volatility in a High Frequency World", Johnson School Research Paper Series No. 9-2011, http://ssrn.com/abstract=1695596
- ^ Investment Risks - Price Volatility
- ^ http://www.wilmottwiki.com/wiki/index.php/Volatility#Definitions
- ^ "Calculating Historical Volatility: Step-by-Step Example". 2011-07-14. http://www.lfrankcabrera.com/calc-hist-vol.pdf. Retrieved 2011-07-15.
- ^ http://papers.ssrn.com/sol3/cf_dev/AbsByAuth.cfm?per_id=17696 Torben Andersen's 40 papers on volatility
- ^ Cumby, R.; Figlewski, S.; Hasbrouck, J. (1993). "Forecasting Volatility and Correlations with EGARCH models". Journal of Derivatives 1 (2): 51–63. doi:10.3905/jod.1993.407877.
- ^ Jorion, P. (1995). "Predicting Volatility in Foreign Exchange Market". Journal of Finance 50 (2): 507–528. JSTOR 2329417.
- ^ Andersen, Torben G.; Bollerslev, Tim (1998). "Answering the Skeptics: Yes, Standard Volatility Models Do Provide Accurate Forecasts". International Economic Review 39 (4): 885–905. JSTOR 2527343. Torben Andersen's attack on Cumby, Figlewski, Hasbrouck, Jorion among many others.
- ^ http://ssrn.com/abstract=226433 Example of working paper attacking volatility forecast skeptics
- ^ http://www.nber.org/papers/w13449 Andersen and Bondarenko's paper, in which they claim superiority over other volatility forecasting models
- ^ http://insight.kellogg.northwestern.edu/index.php/Kellogg/article/the_vix_civ_and_mfiv
- ^ http://papers.ssrn.com/sol3/papers.cfm?abstract_id=970480 We Don't Quite Know What We are Talking About When We Talk About Volatility
- ^ Derman, Emanuel (2011): Models.Behaving.Badly: Why Confusing Illusion With Reality Can Lead to Disaster, on Wall Street and in Life”, Ed. Free Press.
- Lin Chen (1996). Stochastic Mean and Stochastic Volatility – A Three-Factor Model of the Term Structure of Interest Rates and Its Application to the Pricing of Interest Rate Derivatives. Blackwell Publishers.
External links
- Graphical Comparison of Implied and Historical Volatility, video
- Complex Options Multi-Leg Option Strategy Calculator
- An introduction to volatility and how it can be calculated in excel, by Dr A. A. Kotzé
- Interactive Java Applet "What is Historic Volatility?"
- Diebold, Francis X.; Hickman, Andrew; Inoue, Atsushi & Schuermannm, Til (1996) "Converting 1-Day Volatility to h-Day Volatility: Scaling by sqrt(h) is Worse than You Think"
- A short introduction to alternative mathematical concepts of volatility
|
||||||||
|
||||||||||||||||||||||||||||||||||||||